User Area > Advice

Rules for connecting elements

General  |  Degrees Of Freedom For Elements  |  Guidelines For Nodal Connectivity  |  Recommended Element Connectivity

A finite element analysis consists of solving a set of simultaneous (equilibrium) equations which relate structural displacement, stiffness and force. In LUSAS, the force and stiffness terms are evaluated from user information and the displacements are the unknown values. The equation solved is:

f = K a

Where f are the forces, K the stiffnesses and a the displacements. A similar idea applies in field analyses in which potential rather than displacement is the unknown variable.

For structural analyses the displacement at a node will, in general, consist of translational and/or rotational behaviour. Each of these displacement components are termed degrees of freedom. In general three dimensional space there are a maximum of six independent degrees of freedom which are

u, v, w translations corresponding to displacements in the x, y, z axis directions respectively

q_x, q_y, q_z rotations corresponding to rotations about the x, y, z axes respectively

For field analyses there is only one degree of freedom called the potential (F) for all spatial dimensions. That is, one, two and three dimensional field elements each have just the one degree of freedom at each node.

Apart from the obvious distinction between structural and field analyses, the number of degrees of freedom at a node depends upon the element type. It is also governed for some elements by whether the node is positioned at the corner or the midside of the element.

Element nodes from different element types may be connected according to the following general rules

1. For the element node having fewer number of degrees of freedom, these must be in the same order and of the same type as the other connecting element node (for nodes with equal numbers of degrees of freedom the selection is immaterial). For example connecting a GRIL element node (w, q_z, q_y) and a BEAM node (u, v, q_z) is not applicable because the order and type are dissimilar. Connection between an HX8 (u, v, w) and a QSI4 element (u, v, w, q_x, q_y, q_z) is possible since the first three freedoms are of the same type and order

2. Elements having different spatial dimensions (1D, 2D, etc) must not be connected together. For example a BEAM element (2D) and a HX8 element (3D) would be an inappropriate selection

3. Structural and field elements must not be used together at any time

4. The stress types for the connected element nodes need to be compatible. For example, although the degrees of freedom for plane stress and plane strain elements are both identical (u, v), the assumptions made for the stress calculations are totally different and render them incompatible. Similarly, a beam and an axisymmetric element are entirely incompatible

5. For integral element connection (full connection along an element length/edge), matching of the number of nodes of the elements is crucial. 

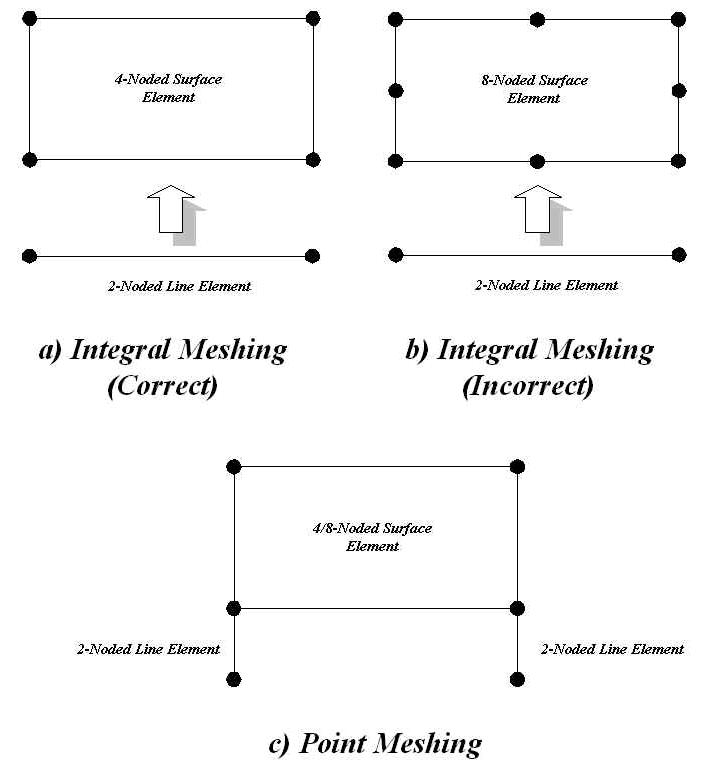
   • The diagram (a) below shows a correct connection in which a two-noded line element is integrally joined to a four-noded surface element - also having two nodes along each side. 

   • Example (b) violates this rule because the line element does not have a corresponding midside node with which to provide mutual connectivity. This would result in a warning, and where possible (within the limits imposed by the other rules), constraint equations would automatically be used to constrain the midside node to the corner nodes as a work around. 

   • Diagram (c) is included to illustrate single point connection at nodes.

The Element Reference Manual provides details of all the elements available in LUSAS and provides the degrees of freedom for each.  There are summary tables for each general element grouping at the beginning of the manual which allow for quick comparison between different elements within the same group or of the same type.

Help > Help Topics > Contents > Element Reference Manual > Element Summary Tables

Integral connection as illustrated above, automatically means that single point connectivity will be possible.  However, there are some cases where single point connectivity alone may be possible.  This can be established from checking corner/end nodal freedoms for the elements to be used together in the Element Reference Manual as well as the Notes regarding use.  With regards to the choice of joint element to use with other elements, there is a section in the Element Reference Manual that gives a table for checking joint compatibility to facilitate the selection of a suitable joint element to use.

Help > Help Topics > Contents > Element Reference Manual > Appendix L : Joint Element Compatibility

The following tables are the recommended element choices when connecting plates or shells integrally with beam elements.

1. This thick beam is recommended.

2. For thin analyses requiring both quadrilateral and triangular elements, this beam is recommended

3. The linear and quadratic 3D Thick Beams (BMI21,22,31,33) have nonlinear capabilities and really combine what 3D Thick Beam (BMS3) and 3D Thick Beam (nonlinear), BTS3 can do individually and effectively supersede both. 

4. The difference between a thin and thick plate or shell element is in the evaluation of through-thickness shear deformation. Thick elements take this effect into account while thin elements do not. Shear deformations, however, would only be of significance in relatively thick sections (refer to any good structural design book for further information). Note that shear deformation is different from shear stress. Shear stress is applicable to both thin and thick elements (varying according to the classical equation dM/dx). However, although through-thickness shear stresses are present in thin elements implicitly, they are not required in the element formulation and, hence, are not evaluated or output

5. There are no associated triangular elements available with this element

6. These thick beam options for single point connectivity to quadratic order, Semiloof thin shells (QSL8, TSL6) at corner nodes only provides translationally connectivity (pinned connection) only.

LUSAS is a trademark and trading name of Finite Element Analysis Ltd. Copyright 1982 - 2022. Last modified: November 29, 2022 . Privacy policy. 
Any modelling, design and analysis capabilities described are dependent upon the LUSAS software product, version and option in use.