User Area > Advice
Orthotropic material constants
Most elastic, engineering problems carried out using the
LUSAS software have isotropic material properties with
two independent elastic constants which are used in the
relationship between stress and strain. This material has
an infinite number of planes of material property symmetry.
A fully anisotropic material (also known as a triclinic
material) will have 21 independent elastic constants and will
have no planes of symmetry for the material properties. A
material with one plane of material property symmetry is termed monoclinic
and has 13 independent elastic constants.
An orthotropic
material has nine elastic constants when modelling a 3D
continuum and has two orthogonal
planes of material property symmetry. The engineering
constants which must be provided are as follows:
E1, E2, E3
= Young's moduli in 1, 2 and 3 directions respectively
nij
= Poisson's ratio for transverse strain in the j-direction
when stressed in the i-direction, that is:
nij = -ej/ei
For si = s
and all other stresses are zero (a uni-directional stress state
condition)
G23, G31, G12 =
shear moduli in the 2-3, 3-1 and 1-2 planes, respectively.
These material parameters are used to form the Compliance
Matrix, [Sij], which relates strain to
stress, as follows:
[e] = [Sij]
[s]
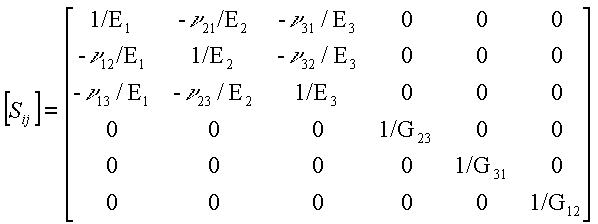
There are nine independent constants because:
Sij = Sji (the matrix is symmetric) and
therefore:
nij/Ei =
nji/Ej
The inverse of the compliance matrix is termed the Stiffness
Matrix, [Cij], which relates stress to
strain and this is also a symmetric matrix.
The orthotropic material constants above are related in such
a way that the laws of physics are obeyed and energy is not
created. Both the compliance matrix and the stiffness
matrix which use these material parameters must
be positive-definite which, in turn, leads to the fact that all
leading diagonal terms of both matrices are positive.
Other conditions which must be satisfied and which arise from
the relationship between the compliance matrix and the stiffness
matrix are as follows:
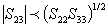
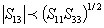
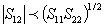
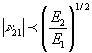
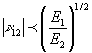
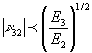
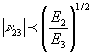
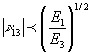
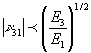
A spreadsheet
can be used to check the above conditions are satisfied and also
carries out other checks on the material data. The
spreadsheet ensures that a proposed set of orthotropic
elastic material constants is valid and does not violate any
physical law. The nine parameters are entered in the
unprotected data-cells at the top of the spreadsheet and various
checks are then carried out on the data. The stiffness
matrix is produced and should any messages such as "bad
value" or "violation of orthotropic law" arise,
then the set of parameters is invalid.
Please refer to the following reference for further
information on orthotropic elastic material constants:
JONES, ROBERT, M. (1975). "Mechanics of
composite materials", Taylor and Francis.
|