User Area > Advice
Nonlinear Iterative Solution Procedures
Linear analyses enforce the assumption that the
stiffness of the structure does not change throughout the solution. This means that the
stiffness matrix need only be evaluated and inverted once, the displacements for any
number of loadcases being computed directly from the static finite element equilibrium
equation:
d = F K-1
For nonlinear analyses, it is no longer possible to obtain a solution that equilibrates
a set of external loads with the internal stress and strain field in such a direct "one-step"
manner. This is because the stiffness of the structure may change at any stage. In this
case a solution procedure is adopted in which the load is applied gradually over a number
of increments, enabling a continual "tracking" of the structural response.
Within each load increment a linear prediction of the nonlinear response is initially
made and subsequent iterative corrections are performed in order to restore equilibrium by
the elimination of the residual or "out of balance" forces. The iterative
corrections are referred to various convergence criteria that control to what extent
equilibrium has been achieved. Such a solution procedure is commonly referred to as an
incremental-iterative (or predictor-corrector) method.
In LUSAS, the nonlinear solution is based on the
Newton-Raphson iterative procedure.
Specification of nonlinear procedures (via the loadcase properties) does not generate,
of itself, a nonlinear response in a structure. It simply invokes the solution procedures.
Thus if no material, geometric or boundary condition nonlinearity is specified, a linear
solution will be produced.
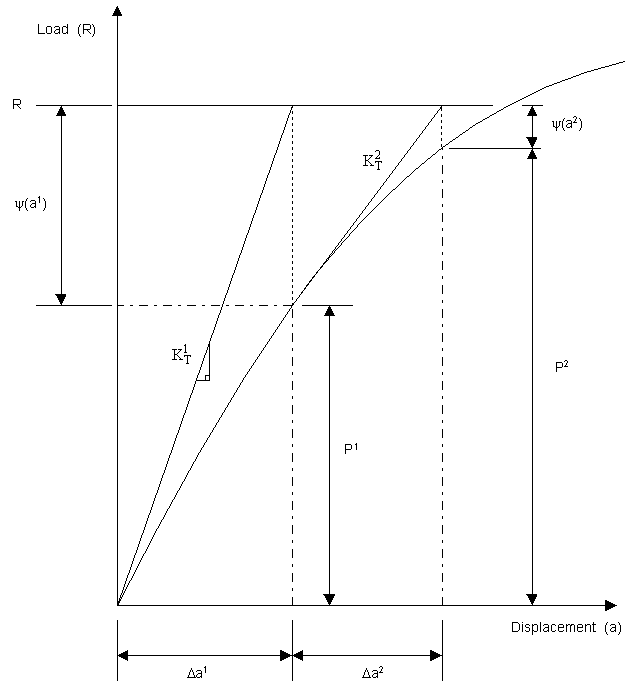
In this procedure the initial prediction of the incremental solution is
based on the tangent stiffness (KT1) from which incremental
displacement (Da1) and the corresponding iterative
force corrections [y(a1)] may be computed.
Subsequent iterative calculations use the current tangent stiffness. In the figure below,
the initial tangent stiffness (KT1) is evaluated and the incremental
load (R) is applied. This load-stiffness combination produces an iterative displacement (Da1)
that does not generally lead to force equilibrium in
the structure and an out of balance residual force is created [y(a1)].
The new tangent stiffness is then evaluated (KT2)
and, in
conjunction with both the applied load (R) and the previous residual force, used to
predict the next iterative displacement (Da2).
The
next residual force may then be evaluated and the procedure continued until the
convergence criteria are satisfied.
Only the tangent stiffness (KT1)
necessarily corresponds to the
elastic modulus, subsequent evaluations will differ according to the degree of
nonlinearity present in the analysis.
Newton-Raphson procedures assume that a displacement solution may be found for a given
load increment and that, within each load increment, the load level remains constant. This
method is, therefore, often referred to as a constant load level incrementation procedure.
Although the Newton-Raphson method generally converges
rapidly, the continual formation and inversion of the tangent
stiffness matrix at the start of each iteration is often
expensive. The need for a robust yet inexpensive procedure
therefore leads to the development of the family of modified
Newton-Raphson methods.
A slow convergence rate may be significantly improved by employing an
iterative acceleration technique. In cases of severe and often localised nonlinearity,
typically encountered in materially nonlinear or contact problems, some form of
acceleration may be a prerequisite to convergence.
In LUSAS, iterative acceleration may be performed by applying
line searches. Essentially, the line search procedure involves
additional optimisation iterations in which the potential
energy associated with the residual forces at each iterative
step are minimised. The added expense of their use is usually
more than offset by their effectiveness in reducing the
number of iterations required for convergence. They are
particularly useful for material nonlinear problems having
localised nonlinearity - especially when using the modified
Newton-Raphson methods.
Line search application is controlled via parameters in
the Solution
Strategy> Advanced... section of the Nonlinear Control
properties.
Line searches are carried out if the absolute value of the line search tolerance factor
(otherwise know as epsln) in the nonlinear iterative log file output exceeds the
line search tolerance factor (toline). The aim is to make the line search tolerance
parameter reasonably small on each iteration to speed convergence and prevent divergence.
See Section 2.3.2.2 in Theory Manual for more details.
In problems where both material and slideline contact nonlinearities are
present, convergence difficulties can arise when evaluating material nonlinearities with
contact conditions that are invalid because the solution is not in equilibrium. To avoid
this situation, contact equilibrium can firstly be established using elastic properties
from the previous load increment before the material nonlinearity is resolved.
This option only has effect in the presence of nonlinear materials and contact. Since
the procedure is designed to deal with contact and nonlinear material interaction it only
applies to those elements that can be used with slidelines (i.e. not bar, beam or plate
elements, etc.). If these other element types have nonlinear material models assigned, the
materially nonlinear behaviour will be computed for both the contact only iterative loop
as well as the subsequent contact and material iterative loop. This parameter is otherwise
known as isilcp and the default is for no separate iterative loops to be invoked.
|