User Area > Advice
Although the Newton-Raphson iteration procedure is stable and converges
quadratically (provided the initial estimate is reasonably close to the solution), it has
the disadvantage that the tangent stiffness matrix requires computationally expensive
inversion during each iteration. Also, it may fail to converge when extreme material
nonlinearities are present in a structure. For this case modified Newton-Raphson iteration
procedures may be more effective.
With modified Newton iterations the current tangent stiffness matrix is replaced with a
previous stiffness matrix, say from the beginning of the increment. This reduces the
numerical cost for each iteration since the inversion of the tangent stiffness matrix is
not required for every iteration. Three common forms of modified Newton-Raphson are:
- KT0 method: The initial stiffness matrix is used exclusively
- KT1 method: The stiffness matrix is updated on the first iteration
of each increment only
- KT2 method: The stiffness matrix is updated on the first and
second iterations of each increment
If arc-length is to be used with modified methods, it is advisable to ensure that the
stiffness is calculated at the beginning of the increment at least. The KT1
procedure is shown in the following figure.
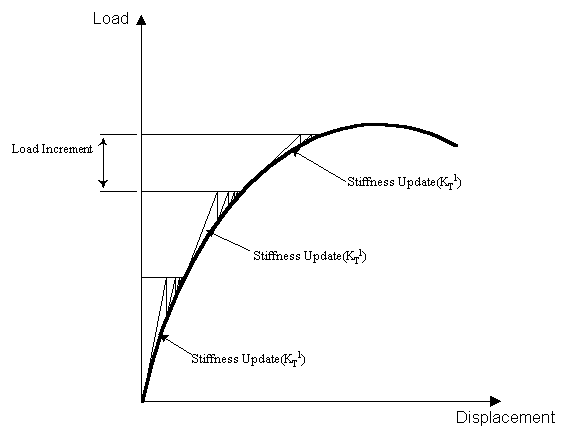
The convergence rate of modified Newton iterations is not
quadratic and the procedure often diverges. However, when
coupled with the line
search procedure it forms an iteration algorithm that
is particularly suitable for structures exhibiting extreme
material nonlinearity. Newton-Raphson iteration is more
effective for geometrically nonlinear problems than modified
Newton iteration.
The choice of standard or modified Newton-Raphson procedures is problem and resource
dependent, although with the swiftly advancing computer technology, issues of
computational resources are becoming increasingly less important and the standard
Newton-Raphson is generally recommended - particularly for geometrically nonlinear
analyses.
A comparative table of the two methods is as follows…
Newton-Raphson |
Modified
Newton-Raphson |
| Iterative stiffness matrix updates |
Less frequent stiffness matrix updates |
| Converges rapidly (quadratically) |
Converges more slowly (linearly) |
| Generally requires few iterations per increment to converge |
Generally requires more iterations per increment to
converge |
| Computationally expensive per iteration |
Computationally inexpensive per iteration |
| May fail under extreme material nonlinearity (e.g. brittle
cracking) |
May be essential for extreme material nonlinearity |
| |
May be assisted using additional "iterative
acceleration" techniques |
|