User Area > Advice
Ill-Conditioned Matrices
The equilibrium equations 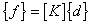 are termed “ill-conditioned” if small
changes in are termed “ill-conditioned” if small
changes in 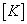 or or 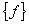 may lead to large changes in the coefficients in
the solution vector may lead to large changes in the coefficients in
the solution vector 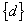 .
.
In general, poor conditioning of the stiffness matrix occurs because
of large variations in the magnitude of diagonal stiffness terms which, in turn, results
from
- A reflection of the physical reality of a structure with a low tangent stiffness because it is near to collapse or buckling
- Large stiff elements being connected to small less stiff elements. An example may be where a stiff beam or joint element is being used to transfer load into the structure. The stiffness of the beam would need to be reduced - typically the beam would only need to be 1000 times the stiffness of the local elements
- Elements with highly disparate stiffnesses. For example, a beam element may have a bending stiffness that is orders of magnitude less than its axial stiffness. Consider a cantilever beam problem that is notoriously problematic with respect to ill-conditioning because of the potential for large differences between the axial stiffness (~EA/L) and shear/rotational stiffness (~12EI/L3) components. The longer the beam, the greater the difference between EA/L and 12EI/L3
Case (1) would be anticipated and the various
nonlinear iterative schemes available in LUSAS would be invoked to obtain a solution.
Cases (2) and (3), however, represent a rather more insidious problem. In these cases, the
physical problem may be extremely well-conditioned, but the modelling in the finite
element model may give rise to ill-conditioning - specifically in the form of
“round-off” and “truncation” errors.
Round-off errors refer to the modification of the last bit of the
computer word in which a number is stored, typically occurring during the solution phase
of the analysis. General experience in finite element analysis, however, has shown that
truncation errors are more important than round-off errors.
A computer stores each floating point or real number in real
“words”. For a double precision application such as LUSAS, two real words are
used to store these numbers. Given that 1 word is equal to 8 Bytes and 1 Byte is equal to
8 Bits, a double precision real number uses 64 Bits to store each real number. Thus only
the leading 64 digits of a number can be stored. It is possible that the information
necessary for an accurate solution resides in the trailing digits of the number which, if
insufficient (that is, truncated) will result in ill conditioning. Condition the following
example of two spring elements joined in series and subjected to a force load P.
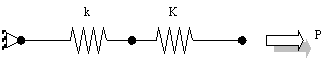
The stiffnesses of the springs are k and K respectively. The global
stiffness matrix KG for the assemblage is as follows
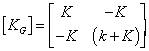
and its inverse as
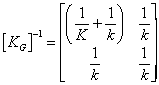
Consider the situation of two equal stiffness magnitudes of k=10 and
K=10. The matrices become
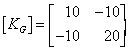
and
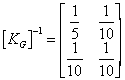
[KG] is, thus, non-singular and would be termed well
conditioned. If k=0.001 and K=10, the global stiffness matrix, as represented by a
computer that handles real numbers to at least 5 significant figures, is
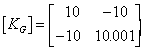
The same matrix given to a computer that uses only 2 significant
figures would render it thus
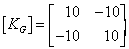
Which is a singular matrix, cannot be inverted to achieve a solution
and is termed ill conditioned because the solution is, by implication, sensitive to
changes in the 5th digit of the stiffness matrix coefficient (k+K). A solution
is only possible if the computer used sufficient bits per real word to ensure that the
stiffness k is not lost in comparison with the larger stiffness K.
This simple example is an instance of the general comments (2) and
(3) given above. A more obvious example of this is given in the following diagram in which
mesh refinement has been applied in rather a severe manner.
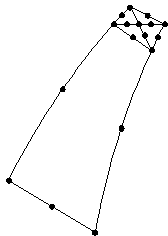
The remedy to this particular case is a more gradual mesh transition
between the two areas.
Truncation errors thus have the tendency to shift essential
information to the latter bits of the computer storage. Even for the ubiquitous 32 Bit
desktop processors such errors are possible – particularly so in such numerically
demanding software applications as finite element analysis.
It is worth noting that, because the axial stiffness of a beam
element is inversely proportional to its length (~EA/L), mesh refinement can increase the truncation error by exacerbating the
difference between the adjacent, disparate stiffness elements. This is even more the case
with the shear/rotational stiffness terms that vary as the inverse of the cube of element
length (~12EI/L3).
The consequences of an ill-conditioned
stiffness matrix will be seen in a number of warning and
error messages relating to zero,
small or
negative
pivots, diagonal
decay or a large condition number. It cannot be emphasized
too strongly that all results from analyses containing such
warnings should be checked particularly carefully, although
it is important to realise that an ill-conditioned system
of equations does not necessarily lead to such large coefficient
changes since the displacements may be sensitive to some
types of change in stiffness or applied force but not to
others.
A numerical measure of the degree of ill-conditioning present in a
stiffness matrix is the condition number. The condition number k of a symmetric matrix [k] can be related to its
extreme eigenvalues.
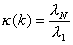
The significance of the condition number is that for stiffness matrix
coefficients kij manipulated with d significant figures, the computed results will be
accurate to s significant figures, where
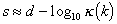
Consider the ill conditioned example above (k=0.001, K=10).
Performing an eigenvalue analysis of the stiffness matrix and extracting the minimum and
maximum eigenvalues can obtain the condition number. The result is a condition number of
40,000. For a computer that can only handle 5 significant figures in the calculations, the
accuracy of the computed results will be given by
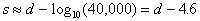
That is, the computer must manipulate the finite element solution
with at least 6 significant figures to obtain at least 1 significant digit accuracy in the
final solution (the closest integer value). Any less than 6 significant figures will
render s as zero or less.
For double precision computing, d=64. Therefore the maximum condition
number to give at least 16 significant figure accuracy is
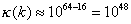
A further disadvantage of a large condition number is that it usually
reduces the rate of convergence of iterative solution methods.
Finite Element Theory Contents
Finite
Element Equilibrium
|