User Area > Advice
The Residual Convergence Criterion
The object of the nonlinear iterative procedure is to restore
equilibrium by the elimination of the residual or "out of balance" forces. The
residual convergence criterion is a measure of these residual forces and is computed from
(Fext - Fint)/Fext, expressed as a percentage. Fext
and Fint are the externally applied loads and corresponding internally
developed forces respectively. This criterion is output to the nonlinear log file as rdnrm.
Although the current value of the convergence criterion should decrease during the
iterative procedure, the decrease is not necessarily monotonic. The following curve is
typical of residual norm behaviour, i.e. oscillating but converging: 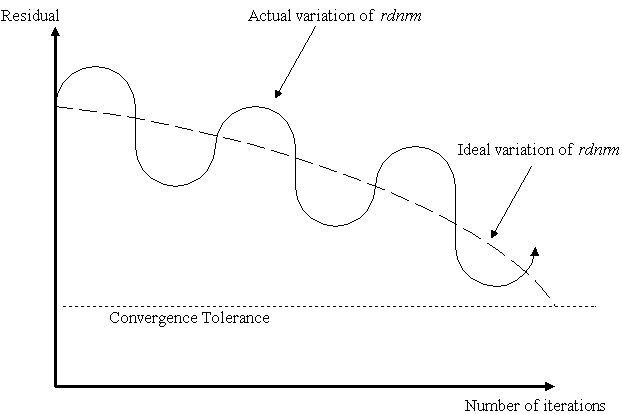
For increments that do not converge, the manner in which rdnrm
behaves can provide valuable indicators to the source of
the problem. For all convergence problems the convergence
checklist should be consulted primarily, but the following
list is separated into the most frequent convergence behaviour
types and their corresponding potential remedies.
| All Convergence
Behaviour: |
- Reduce the load increment
- Check for "pivot" warnings. If present
see the pivot
checklist
- For elements that are simulating "stiff" members, reduce their
stiffness (round-off problems)
- Reduce slideline stiffness coefficients ("normal" chatter)
- Reduce friction coefficient ("tangential" chatter)
- Improve the aspect ratios of poorly shaped elements
- Use consistent units throughout the analysis
- Point loads and supports can promote severe local plasticity. Either
distribute the load/support effect over a number of nodes or define elastic properties in
the area to eliminate the material failure
- An element mechanism may have been excited. The remedy is to invoke fine
integration
|
| Slow Convergence
Behaviour: |
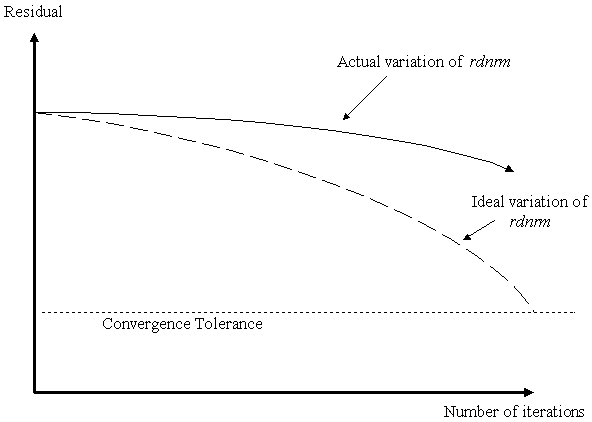
|
|
- Decrease the threshold for
the line search technique to be automatically
invoked and increase the maximum number of line
searches to 5
- Ensure that
Newton-Raphson
iterations are being performed rather than modified
Newton-Raphson
- Increase the number of iterations per increment. Slideline analyses,
particularly, can require a significant number of iterations in the first few iterations
of an analysis
|
|
|
| Oscillating Convergence
Behaviour: |
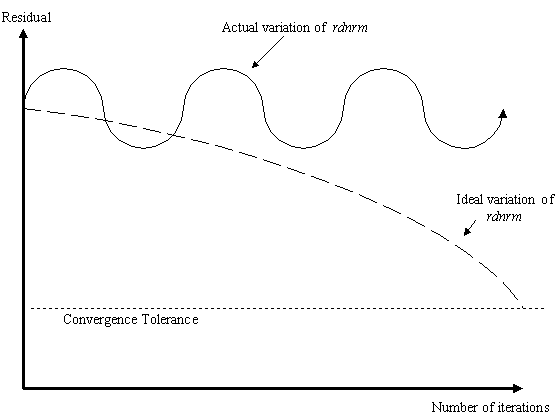
|
|
- Split up any slidelines that traverse sharp angles (e.g. greater than
45-90 degrees)
- Invoke the slideline extension facility, particularly for irregular
slideline surfaces
- Refine the mesh in the area of slideline definitions. Coarse meshes can
produce single point contact and promote instability
- Has merging/equivalencing been performed fully? There may be a crack in
the mesh
- Check the support conditions will prevent rigid body motion
- If a geometrically nonlinear
analysis is being carried out, try invoking
"guide
arc-length by current stiffness parameter"
- Mesh refinement may be helpful for more coarse definitions
|
|
|
| Fixed Convergence
Behaviour: |
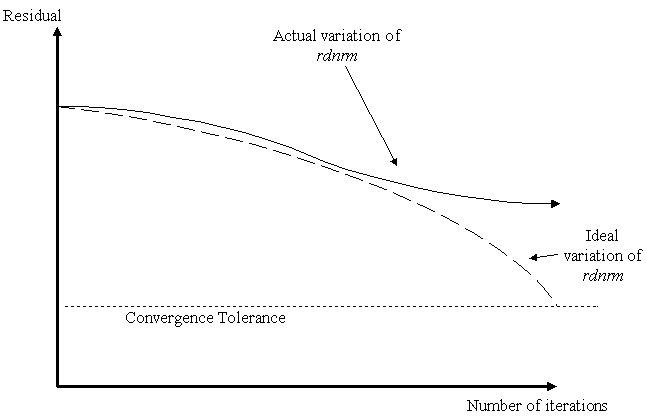
|
|
- If the concrete material model is being used, slacken the residual norm
- Massive plastic strain development with a highly constrained structure
can cause locking
- Large plastic strains with 3-noded triangular elements can cause locking.
The remedy is generally to use the corresponding 6/8-noded elements with fine integration
- Check the material properties if there is more plastic strain developed
than expected
- If the concrete material model is being used, slacken the convergence
tolerance to 5
|
|
|
| Divergent Convergence
Behaviour: |
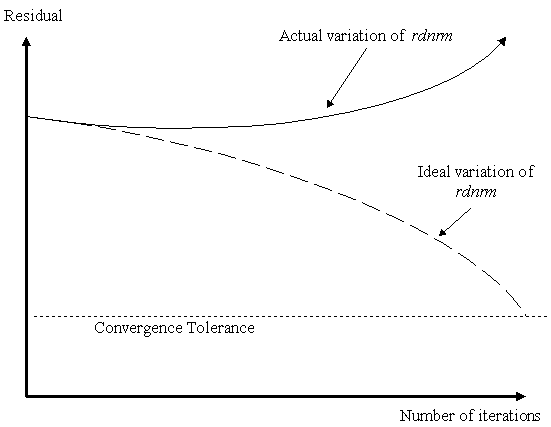
|
|
- Is geometric nonlinearity required? Large deformations/rotations may be
causing non-physical stiffening
- Are the convergence criteria too slack? Tighten the convergence criteria
- particularly for geometric nonlinearity
|
|