User Area > Advice
Jacobian Matrix
The Jacobian
matrix is an important component of the isoparametric element formulation. It is commonly
denoted as [J] and represents a “scaling” factor between the derivatives of the
natural and the local coordinate systems.
To
help explain its use, consider a 3-noded bar element, the
natural coordinate
system for which is as follows
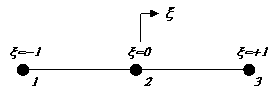
The coordinate
variable x (xi)
thus varies between -1 and +1 and it effectively represents a “normalised coordinate
system. The local coordinate system for the same element, however, is specified as
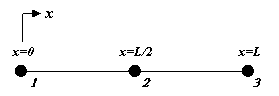
The coordinate
variable now varies in the range 0 to L.
For
a number of reasons
it is beneficial to derive the element matrices in terms
of the natural coordinate x.
However, when formulating finite elements it is frequently
necessary to obtain the results for the derivative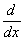 
and the chain rule is used as follows
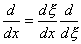
The Jacobian is
then defined as
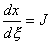
Giving the
correspondence
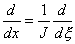
The
Jacobian can then be seen to relate the natural coordinate
derivatives to the corresponding local coordinate derivatives.
The isoparametric
formulation relies on there being a one-to one relationship
between the natural and the local coordinate systems (and
their derivatives), that is, there is a unique mapping between
the two system.
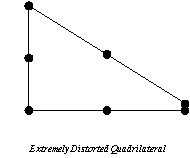
To detect any
original element geometry or subsequent deformations that violate this requirement, the
magnitude and (particularly) the sign of the Jacobian determinant have been found to be
very effective. Determinants equal or close to zero would imply a “collapsing”
element, i.e. a quadrilateral having one of its edges squashed to form a triangular shape,
such as
For non-zero,
positive values, the Jacobian determinant represents a measure of the Gauss point volume,
that is,
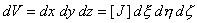
Should the
determinant of the Jacobian at any Gauss point be evaluated as negative, errors due to
non-uniqueness of mapping are indicated, which means that an unacceptable element shape is
present in the mesh, such as
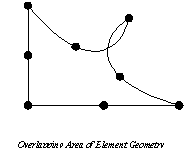
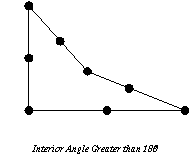
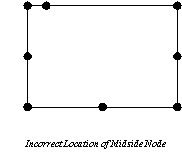
In the last
case, the midside nodes need to be in the middle half of the element sides, although the
middle third is safer.
In MODELLER, the meshing algorithm used ensures that the element
geometry will not violate this condition, but it is possible
when performing a geometrically nonlinear analysis. Should
an “Illegal Jacobian” error be encountered during
an analysis, a checklist
of possible causes is available.
Finite
Element Theory Contents
Local
Coordinate System
Isoparametric
Finite Element Formulation
|
