User Area > Advice
Natural Coordinate System
In order to make the finite element method
as generally applicable as possible, a natural coordinate system is required. Typically it
is specified in terms of (x) for line elements (bars, beams), (x, h) for surface elements (plates, plane membranes) and (x, h, z) for volume elements (solids).
The coordinate axis (x,h,z) are curvilinear coordinates and can be thought of a
representing the more usual Cartesian system (x,y,z) locally within the element. The
natural coordinates are chosen such that each coordinate axis varies between –1 and
+1 irrespective of the actual dimensions of the element – in essence this is a
normalised coordinate system.
This
natural coordinate system permits the use of numerical
integration and allows element integrals to be performed
over simple and predetermined limits rather than over the
limits determined during the solution as a result of element
deformation and geometry change. The use of numerical integration
immediately renders a tremendous flexibility to the finite
element method – making it applicable to many different
classes of problem in all scientific disciplines. The natural
coordinate system also facilitates the use of element shape
functions and their associated benefits, together with
a vast range of elements that may be formed easily from
a standard set of basic equations, rather than a new basis
for each element.
A typical one-dimensional natural
coordinate system for a two-noded line element is represented as follows
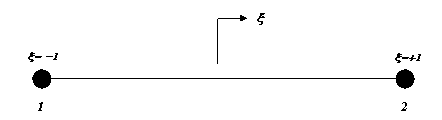
And for a
three-noded line element as
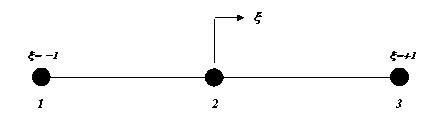
The coordinate system is “fixed”
to the element and deforms with it such that, for example, the x coordinate for a bar will, at all points, be along the length of
the bar. The origin of the system is at the centre of the element (x=0).
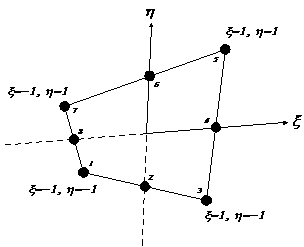
For two dimensional elements, the natural
coordinate axes (x, h) are used which have their origin at the centre of the element (x=0, h=0) and pass through the midpoints of the opposite sides. They
need not be orthogonal or parallel to any global coordinate system.
The natural coordinates for such a plane element are given in the
following diagram. Note that their orientation is determined by the element node
numbering.
Finite
Element Theory Contents
Shape
Functions
Isoparametric
Finite Element Formulation
Numerical
Integration
|