User Area
> Advice
Using joints: Spring stiffnesses
Using Joints: Mesh
| Geometric
attributes | Material
attributes | Spring
stiffnesses | Supports
| Loadcase properties
A spring stiffness is required in the definition of joint or spring support attributes in
LUSAS.
Spring stiffness, k, is as defined in Hooke's law, viz. F=k*x where F is an applied force and x is the resulting displacement. It follows that where a
known displacement (x) for a known force (F) is available, the spring stiffness entered in the dialog box, k = F/x.
Similarly, the spring stiffness for any rotational stiffnesses
required should be based on a Hookean model, viz. M = kØ, and
rotational spring stiffness will be specified in moment/
radians.
In many cases the joint represents a specific medium in the
structure and the stiffnesses should be calculated accordingly. Derivations of spring
stiffnesses appropriate to a "modulus of subgrade reaction"
or other specialised theorem, are not considered in this article.
In other cases, the joint represents a part of the structure.
In such a case, engineering theory can be used to derive equations for k based on the structural member which the spring is intended to model
(appropriate to each degree of freedom in the joint
material attribute). The notes below are intended as an
example considering a specific (but common) case.
Sometimes it is necessary to use a joint element to model a "fixed"
or "free" condition (e.g. to mimic the action of a tension-only member
or contact).
However, for a "fixed" condition, you cannot enter a stiffness of infinity, so you should use a high stiffness.
For a "free" condition, you may not be able to enter a stiffness of zero, so you may use a low stiffness. Zero may be entered but may cause numerical instability, depending on the solution method selected.
In the case of modelling contact
for example (lift-off
support/connection), the joints do not model
a structural element and so there is no associated length, they
just model the contact interface – the stiffness is input
directly and the joints should ideally be meshed with coincident
end nodes. If the joint
is modelling something arbitrarily stiff or flexible (in the case
of modelling contact or a hinge connection for example) then the
key is to make the joint stiffness much stiffer or much more
flexible relatively speaking to the elements it connects to.
The notes below give further guidance to model a "fixed"
or "free" condition using simple and approximate calculations for the
stiffness of an adjacent element as a basis for deciding what
order of magnitude of stiffness in the joint would be considered
very stiff or very flexible in comparison. The use of
precise numbers to carry out a precise calculation is therefore
not necessary; the approximate values determined are then factored
arbitrarily up or down by something like 1E3 or 1E6 to get
something relatively very stiff or very flexible
respectively. The reason for this approach is to avoid extreme
high/low stiffnesses as these may cause ill-conditioning and
convergence problems in a nonlinear solution.
Note that in the case of modelling
a bearing, connector or connection arrangement, the question is
not what the length of the joint is, but what is the geometry and
material of the connection component/arrangement it is to
represent. If a joint is simply representing a connector of
constant section and a given length, then the axial stiffness can
be calculated as F/x = EA/L, where L is the length of the member
rather than the joint element. If the joint represents
something more complex, then the calculations below would not
suffice – a component like a bearing may have stiffnesses
published by the manufacturer for example.
Spring stiffnesses for joints
between point features or at line ends
If the spring stiffnesses were intended to model a
thin beam (assuming beam theory):
Axial: Ka = EA/L, (typical units kN/m, N/mm etc)
Lateral: (one end fixed and the loaded end
guided): Kh = 12EI/L³ (typical units kN/m, N/mm etc)
Rotational: Km = EI/L (typical units
kNm/rad, Nm/rad etc)
Torsional: Kt =
GJ/L (typical units
kNm/rad, Nm/rad etc)
In a case where the stiffness specified is to model a "fixed" or
"free" condition, in principle, the stiffnesses should be high or low relative
to the rest of the structure, in particular adjacent members. A good
starting point for the estimation of a suitable spring stiffness might therefore
be:
- For a "fixed"
condition, first use approximate calculations for Ka, Kh, Km
and Kt (using the above equations for example) to determine the
stiffnesses of the most stiff adjacent member, then
factor each stiffness by a large number such as 1E3 or 1E6
to be input for the joint to ensure that it is much stiffer.
- For a "free" condition,
first use approximate calculations for Ka, Kh, Km and Kt
(using the above equations for example) to determine the
stiffnesses of the least stiff adjacent member, then
factor each stiffness by a small number such as 1E-3 or 1E-6
to be input for the joint to ensure that it is much less
stiff.
|
|
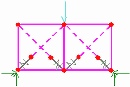
Mesh attributes for joints
between line features (or edges of surfaces)
When assigned to line features, which have a calculable length, forces in
the equation F=k*x are
per unit length and spring stiffnesses should be likewise (typical units therefore
kN/m², N/mm² etc). If the spring stiffnesses were intended to model a
cantilevering "slab":
- In plane of slab: Kx =
EA/L. A is per unit length of
cantilever tip, viz. A=thickness t
- Lateral (along edge of slab): Ky =
Gt/L based on shear deformation. For isotropic elastic materials, Shear modulus G=E/[2(1+v)]
- Lateral (normal to slab): Kz =
12EIyy/L³. Iyy is per unit length
of cantilever tip viz. Iyy=t³/12
-
Torsion about local x: KTHx = CG/L where C=t³/6 generally
- Rotation about local y: KTHy =
EIyy/L I is per unit length
- Rotation about local z: KTHz =
EIzz/L I is per unit length
In a case where the stiffness specified is to model a "fixed" or
"free" condition, in principle, the stiffnesses should be high or low relative
to the rest of the structure, in particular adjacent members. A good
starting point for the estimation of a suitable spring stiffness might therefore
be:
- For a "fixed"
condition, first use approximate calculations for Kx, Ky,
Kz, KTHx, KTHy and KTHz (using the above equations for
example) to determine the stiffnesses of the most stiff adjacent member,
then factor each stiffness by a large number such as 1E3 or
1E6 to be input for the joint to ensure that it is much
stiffer.
- For a "free" condition,
first use approximate calculations for Kx, Ky, Kz, KTHx,
KTHy and KTHz (using the above equations for example) to
determine the stiffnesses of the least stiff adjacent member,
then factor each stiffness by a small number such as 1E-3 or
1E-6 to be input for the joint to ensure that it is much less
stiff.
|
|
Mesh attributes for
joints between surface feature faces
When assigned to surface features, which have a calculable face area, forces in
the equation F=k*x are
per unit area and spring stiffnesses should be likewise (typical units therefore
kN/m³, N/mm³ etc). If the spring stiffnesses were intended to model a
cantilevering "slab":
- Perpendicular to joint: Ka =
EA/L based on in-plane ("axial") deformation. Since
Ka will be per unit area, assigned to a surface feature,
'A' may be taken as unity in many cases.
- Parallel to joint: Kh =
3EI/L³ based on flexural deformation of slab (minor bending axis). Since
Kh will be per unit area, assigned to a surface feature,
'A' should be divided through. An effective area may need to be assumed.
- Lateral to joint: KL = Gt/L based on shear deformation. For isotropic elastic materials, Shear modulus G=E/[2(1+v)]. Since
KL will be per unit area, assigned to a surface feature,
't' may be taken as unity in many cases.
In a case where the stiffness specified is to model a "fixed" or
"free" condition, in principle, the stiffnesses should be high or low relative
to the rest of the structure, in particular adjacent members. A good starting point for the estimation of a suitable spring stiffness
might therefore be:
- For a "fixed"
condition, first use approximate calculations for Ka, Kh,
and KL (using the above equations for example) to determine the
stiffnesses of the most stiff adjacent member, then
factor each stiffness by a large number such as 1E3 or 1E6
to be input for the joint to ensure that it is much stiffer.
- For a "free" condition,
first use approximate calculations for Ka, Kh, and KL (using
the above equations for example) to determine the
stiffnesses of the least stiff adjacent member, then
factor each stiffness by a small number such as 1E-3 or 1E-6
to be input for the joint to ensure that it is much less
stiff.
|
|
The joint strain (relative displacement between its nodes) can be checked (using a Contours or Values post-processing layer).
View > Drawing Layers > Contours >
choose "Entity" as "Strain - " following by the joint type used, and then select the appropriate "Component" as
Ex, Ey or Ez depending on which direction is the lift-off/contact contact direction
For strain in a direction that was intended to be
"fixed" the amount of strain should be checked as being negligible for
each direction (for contact or for a rigid connection or bond for example). Where modelling contact, the strain in the normal direction between contacting surfaces would represent a penetration between those surfaces and
so the stiffness can be adjusted if required to reduce this. In the case of a gap, you can check that the joint strain does not exceed the gap
(meaning that the gap has closed but with negligible penetration) and increase the contact stiffness if it does.
The image below shows a check for
the contact stiffness where there is too much penetration and the
contact stiffness needs to be increased:
The joint force/moment in a
direction that was intended to be "free", can be
similarly checked as being negligible in the case of lift-off or for a hinge rotation for example (or other freedom intended to have low/zero stiffness) and again the stiffness adjusted if required to
reduce that spurious force/moment for the relevant freedom.
View > Drawing Layers > Contours >
choose "Entity" as "Force/Moment - " following by the joint type used, and then select the appropriate "Component" as Fx, Fy or Fz depending on which direction is the lift-off/contact contact direction
The image below shows a check for
the lift-off stiffness where there is too much tensile force in
the joint and the lift-off stiffness needs to be reduced:
The image below shows both contact
and lift-off stiffnesses corrected to give little tensile force in
the lift-off direction and little penetration in contact:
How do I model
lift off supports? (main page)
How
do I model tension only members? (main page)
How
do I model a hinged connection between shell meshed
surfaces? (main page)
|