User Area > Advice
Evaluating the element mass matrix
The element mass matrix is evaluated from
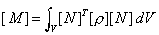
For
a 3-noded
bar element, the shape
function is defined as
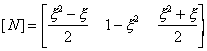
Since
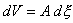
The mass matrix is given by
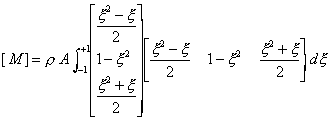
After expanding, becomes
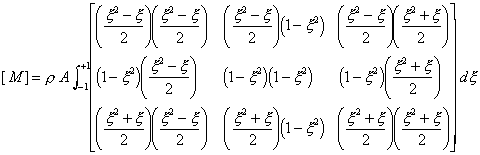
Multiplying out the bracketed
terms gives
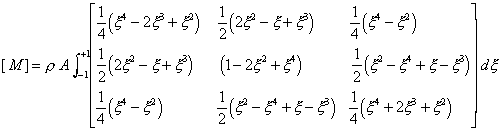
This shows that integration of order
four is required for the mass matrix of such a bar element.
Because a Gauss integration
rule of order n integrates exactly a polynomial of order
(2n-1), the mass matrix will be integrated accurately using
a 3-point rule ([2*3]-1 = 5)
This is in comparison with the stiffness
matrix, given
by
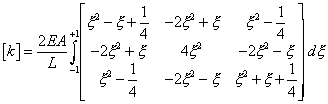
Which is of order two and only requires a Gauss rule of order 2
([2*2]-1 = 3).
Hence, for a consistent mass matrix the
full integration
rule as used for the stiffness is appropriate. This is the
case because the consistent mass matrix is obtained from
the shape functions [N] directly rather than their derivatives
(i.e. the [B] matrix), as in the case of the stiffness and
force matrices.
For lumped mass matrices, only the volume strictly needs to be
accurately obtained. In LUSAS, however, the lumped mass matrix is typically evaluated from
a summation of the consistent mass terms - hence the same order of integration rule is
used regardless of the type of mass matrix specified. The few exceptions to this rule are
typically indicated when the default and fine integration rules are the same –
notably in the case of the QSI4/SHI4 shell elements. For these elements, the lumped mass
matrix is evaluated directly; hence higher order rules do not need to be invoked for mass
evaluations.
It is for this reason that the fine integration rule is invoked
automatically for dynamic analyses to ensure that the mass matrix is evaluated correctly.
Note that this is not necessary when using Constant Body Force to apply self weight
loading in a static analysis, since this effectively applies a lumped mass - the exact
volume being evaluated readily with the default integration scheme used.
See Theory Manual 1 for more information on mass matrices,
specifically the difference between consistent and lumped matrices.
Finite Element Theory Contents
Shape Functions
Isoparametric
Finite Element Formulation
Numerical Integration
|