User Area > Advice
Numerical Integration
An important aspect of the
finite element method is the requirement for numerical integration. For example, the
stiffness matrix [k] and load vector {r} needs evaluating for each element as follows
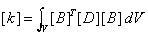
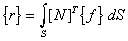
Where [N] and [B] are the shape function
and strain-displacement
matrices respectively.
It is possible to evaluate such integrals using closed form analytical
solutions for a few element types (see explicit
integration), but
this would, in general, reduce the flexibility of the finite element method both dramatically and
unnecessarily. Numerical integration provides a convenient and efficient method to carry
out such integration and, with appropriate use, yields extremely accurate results.
There are two numerical integration methods used in LUSAS
In
the Newton-Cotes method the integration points are equally spaced along the natural
coordinate axes for the section, typically at the nodal positions. In the Gaussian
integration method, the integration points are not equally spaced along the natural
coordinate axes for the section, but are at internal element positions called Gauss
points. In the latter case, the positions of the integration points have been optimised to
give a more efficient method than the Newton-Cotes method, albeit not at as convenient
integration positions. The methods are, however, actually very similar in practice.
Consider a line element, in which the one-dimensional integral is
required as follows
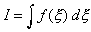
The numerical integration is given for this as
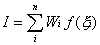
Where
Wi are known as the integration
weights and the f(xi)
are the values of the function at the pre-determined integration points.
For
this line element the integration point positions and the corresponding integration
weights for the different integration rules of the Newton-Cotes method are given in the
following table
Integration Rule |
Integration Point Locations |
Integration Weight |
1 Point Rule |
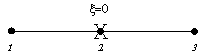
|
2.00000 |
2 Point Rule |
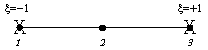
|
1.00000 |
3 Point Rule |
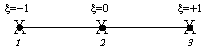
|
0.33333
1.33333
0.33333 |
Similarly, the integration point positions and the
corresponding integration weights for the different integration rules of the Gaussian
method appropriate to this line element are given as follows
Integration Rule |
Integration Point Locations |
Integration Weight |
1
Point Rule |
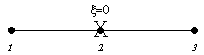
|
2.00000 |
2
Point Rule |
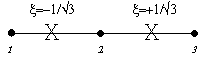
|
1.00000 |
3
Point Rule |
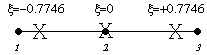
|
0.55556
0.88889
0.55556 |
Similar rules apply for surface and volume elements. See
appendix A of the theory manual for more information.
As
an example of the use these numerical integration schemes, consider the following integral
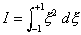
The analytical solution is readily available as
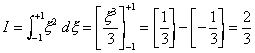
Using the Newton-Cotes integration method we have, for the
one-point rule
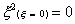
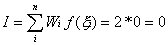
Where 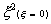 .means the function x2
is evaluated at x=0. .means the function x2
is evaluated at x=0.
For
the two-point rule, this becomes
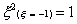
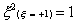
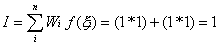
And for the three-point rule
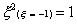
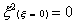
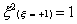
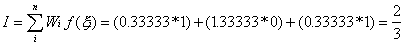
Using the Gaussian integration method we have, for the one-point
rule
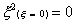
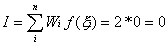
For the two-point rule
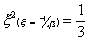
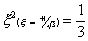
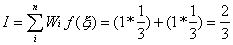
And. for the three-point rule
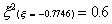
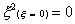
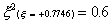
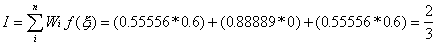
It
can be seen that the Gaussian method exactly integrates the equation with the 2-point
integration rule, whilst the Newton-Cotes method requires a 3-point rule. Specifically, a
Gaussian rule of order n integrates exactly a polynomial of order (2n-1) whilst the
Newton-Cotes rule of order n integrates exactly a polynomial of order (n-1). In general,
Gauss integration is the more efficient since a given order of integration may be
performed with less integration points than for the Newton-Cotes methods (a direct result
of the optimised Gauss point locations). This is important since such integrals form a
large part of the cost of a finite element analysis.
In
LUSAS, Gaussian integration is the most prevalent method. The Newton-Cotes method is used,
however, where stress results are particularly required at nodal positions. This is the
default case for delamination elements and optional for the integration of variables along
the length of cross section beams. It is the default case when integrating the rigidity
matrix through the depth of cross-section beam elements (the default integration employs a
3x3 Newton Cotes rule for linear materials and a 5x5 rule for nonlinear materials). More
information on the cross sectional integration for these elements is available in the
Element Reference Guide.
The
appropriate order of integration rule to use for an element depends on the matrix that is
to be evaluated and the specific element being considered, but it does need to consider
the following issues
a) If
a high enough integration rule is used, all matrices will be evaluated very accurately.
However, the cost of an analysis increases significantly when higher order rules are used
than are strictly necessary. This is because the integration of all the element matrices
in the finite element method are performed at each Gauss point – the more Gauss
points, the more numerical loops are required
b)
Using too low a rule may integrate the matrices very
inaccurately, such that they contain rigid
body modes or mechanisms.
Such behaviour affects the results to a very large degree
An element is said to be fully
integrated if the integration rule used is the lowest order required to evaluate the
element matrices as accurately as an analytical integration and also ensure that there are
no element mechanisms associated with the element. Conversely, an element is said to be
under-integrated if the integration rule used is the lowest order required to evaluate the
element matrices as accurately as an analytical integration but retains one or more
element mechanisms associated with the element. There are good reasons for
under-integration that are discussed further later.
In considering, for example, the correct integration rule required for
a 3-noded bar element, the stiffness matrix can
be evaluated from the following, between the natural
coordinate limits of ±1.
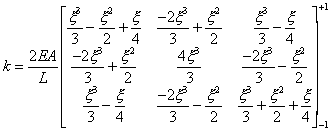
Which
is clearly a cubic or 3rd order matrix. Since a Gaussian rule of order n
integrates exactly a polynomial of order (2n-1), this stiffness matrix will be fully
integrated with a Gaussian rule of order 2. It is usually good practice to evaluate the
other element matrices with the same order (e.g. the forces).
The
mass matrix is, however, dealt with slightly differently. For more information, see Evaluating Mass Matrices.
In
the LUSAS Element Reference manual, there is a section entitled “Integration
Schemes” that describes the integration rules used for each element. An example is in
the following table, from the two-dimensional plane stress element section
Stiffness |
Default |
1-point
(TPM3), 3-point (TPM6)
2x2
(QPM4, QPM8)
|
|
Fine
(see Options) |
3x3
(QPM8), 3-point (TPM3) |
Mass |
Default |
1-point
(TPM3), 3-point (TPM6)
2x2
(QPM4, QPM8) |
|
Fine
(see Options) |
3x3
(QPM8), 3-point (TPM3) |
In
this section, the “default” integration rule is specified for each element
within this element suite. The integration locations for the 2x2 and 3x3 rules (and
others) are described in the appendix of the element reference manual.
The term “fine”
integration actually means “full” integration. For some elements, the
“fine” integration rule will be the same as the default rule. This means that
the default rule used is the “full” integration rule - that is, the integration
rule that yields accurate results without element mechanisms present. For others, the
default and fine rule will be different. In such cases, the default rule used
under-integrates the element matrix and is called a reduced
integration rule.
Reduced integration has been
found most effective in a number of element types. This is not an uncommon approach and is
based on substantial experience. Any mechanisms present from such a usage are not commonly
experienced in a typical linear element assembly although they may occur in both
materially and geometrically nonlinear analyses. When investigating the analysis results,
checks should be performed for spurious stress oscillations and peculiarities in the
deformed configuration that may indicate the presence of an element mechanism.
The benefit of
reduced-integration is typically that under-integration of the stiffness matrix prevents
locking, which may occur with full integration when either the element is subjected to
parasitic shear for example or as the material reaches the incompressible limit in the
presence of material nonlinearity. Locking produces an over-stiff solution, most
significantly affecting the bending and/or shear results. Locking can, however, be
significantly suppressed with the higher order rules when using a fine mesh discretisation
(unfortunately leading to costly analyses). For elements that use a reduced rule by
default, the NOTES section in the Element Reference Manual describes the specific reasons
for this choice of integration rule.
The fine integration option for
an element may be invoked within MODELLER using File> Model Properties> Solution>
Element options.
There
are also a number of non-standard integration rules that have been developed for specific
elements, these include the 5-point rule for the Semiloof thin shell elements and the 13
and 14-point rules for the 3D continuum solid element.
Implication: Evaluating Mass and Damping Matrices
In
LUSAS, for dynamic analyses, fine integration is invoked automatically to ensure that the
mass and damping matrices are fully integrated. They are generated as follows
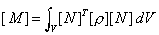
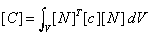
From
which it can be seen that the element mass and damping matrices are evaluated directly
from the shape functions [N], rather than their derivatives (as in the case of the other
element matrices), and therefore requiring a higher order rule. See evaluating mass matrices
Implication:
Element mechanisms - What are
they?
Reduced
or under-integration can provide an improvement to element behaviour. It does pose,
however, a numerical difficulty in that one or more element mechanisms may be associated
with the element.
Additional
Links…
|