| Background
Numerical modeling of concrete has
a history that spans more than three decades, during which time
considerable advances have been made in both the underlying
theories of the constitutive models as well as in the practical
capabilities of finite element codes for concrete analysis. The
development of the new LUSAS concrete model has extended the
analytical capabilities for modelling concrete cracking and
crushing to a new level and can model a complete range of concrete
characteristic behaviour in a consistent and robust manner. It is
seen by many in the field to be one of, if not the leading
concrete material model available today.
Planes of Damage
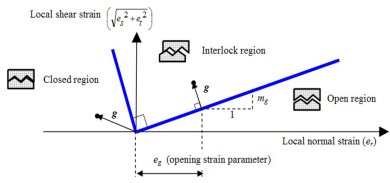 The LUSAS concrete model simulates
directional cracking, crack closure and shear contact (or
aggregate interlock) behaviour in an integrated manner, while
accounting for the type of damage and triaxial frictional response
that characterises the behaviour of concrete in compression. In
order to achieve all of these these aims within a
thermodynamically consistent framework the model calculates
directional damage planes that at some point in a loading process
become fixed in direction. However, a problem in deriving a model
that predicts directional damage is how to simulate complete loss
of strength in one direction whilst maintaining strength in other
directions. This and other difficulties are well known to those
involved with concrete material model development and some
long-standing concrete material models provide solutions to some
of the problems, however unlike the LUSAS concrete model they do
not address the problem of how to correctly simulate the shear
behaviour of formed macro cracks or fully three-dimensional
behaviour.
In the LUSAS concrete material
model embedded damage-contact planes have been integrated with a
plasticity component by using a thermodynamically consistent
plastic-damage framework. The essential elements of the model are:
- A local stress – strain
relationship, which here is a damage-contact model
- A function from which local
strains can be computed such that the local and global
constitutive relationships are both satisfied. This is termed
the total-local function.
- A triaxial plasticity component
for simulating frictional behaviour and strength increase with
triaxial confinement
- A thermodynamically consistent
global stress-strain relationship
- The model has been developed
with an implicit stress recovery – consistent tangent matrix
algorithm.
Uses
FIB (Fédération Internationale du
Béton) Bulletin 45 "Practitioners guide to finite element
modelling of reinforced concrete structures" states:
"The state of the art in nonlinear finite element analysis of
reinforced concrete has progressed to the point where such
procedures are close to being practical everyday tools for design
office engineers. No longer solely within the domain of
researchers, they are finding use in various applications; many
relating to our aging infrastructure. Nonlinear computer analysis
procedures can be used to provide reliable assessments of the
strength and integrity of damaged or deteriorated structures, or
of structures built to previous codes, standards or practices
deemed to be deficient today. They can serve as valuable tools in
assessing the expected behaviour from retrofitted structures, or
in investigating and rationally selecting amongst various repair
alternatives"
Use of the LUSAS
nonlinear concrete material model can help make a significant
contribution to the assessment of ageing structures and to the
design and long-term management of structural assets.
Validation testing
Over the course of the development
of the LUSAS concrete material model and also after its inclusion
into LUSAS a number of validation and quality assurance testcases
were used to verify its usage against both experimental and
theoretical results. Three representative examples of some of the tests
undertaken are shown here:
- Notch test by Barr and
Brokenshire
- Reinforced concrete beam by
Bresler and Scordelis
- Single edge notched beam, by
Arrea and Ingraffea
|
