 Case Study Case Study
Making the most of Eurocodes for
critical buckling analysis
-
Investigations
into the implications of changing to Eurocodes for bridge design
-
Comparison
of analysis of first and second order effects for critical
buckling analysis
-
Increased
load factors obtained - especially for nonlinear analysis

Atkins,
the UKís largest engineering consultancy, has been carrying out
investigations into the implications of using the new Eurocodes for UK
bridge design. As part of its study finite element test models were
created in LUSAS Bridge to assess particular aspects of the new codes.
From analyses carried out, significant benefits have been seen when
using the new Eurocodes for linear and nonlinear investigations into
critical buckling analysis of steel girder structures with transverse
stiffeners.
Overview
The use of Eurocodes for bridge design
in the UK requires engineers to make greater use of first principles
as fewer rules and formulae are given compared to the BS 5400 code.
The new codes have, in effect, moved away from being equation-based to
becoming more analysis driven, and this, in many cases, will lead to
the greater use of finite element analysis to model particular types
of structures.
First order or second
order?
The default analysis in the new
Eurocodes is second order (nonlinear), and considers p-delta effects.
But, in almost all cases where first-order (linear elastic) analysis with BS
5400 was used previously, first order analysis with the
Eurocodes can be used just as successfully, if not more so. However,
when finite element software with a nonlinear capability is used to
investigate second-order effects, design to the Eurocodes really comes
into its own and great benefits can be obtained both in economy of new
designs and in assessments of existing structures over BS 5400 methods.
Evaluating the
Eurocodes
Atkins carried out trial calculations
for the Highways Agency and other clients on existing concrete and
steel-concrete composite bridges. These trials indicated that, on
average, when the basic application rules are applied the Eurocodes
give a small increase in economy in the design. Chris Hendy, Head of
Bridge Design and Technology at Atkins said: "For concrete structures,
there is a systematic saving in flexural reinforcement and shear
reinforcement for reinforced concrete structures, but generally little
difference for prestressed structures." He continues: "For steel design,
there is more economy to be obtained from using the Eurocodes for
stiffened structures, which reflects a greater confidence in behaviour
as a result of recent testing and of some nonlinear parametric studies
that have been undertaken. Economy can be improved
further if nonlinear analysis with software such as LUSAS Bridge is
employed."
Transverse stiffener
investigation
A model of a plate girder with a
central load was one of many set up by Atkins on behalf of the UKís
Highways Agency to investigate the Eurocode rules for transverse
stiffeners resisting shear. The model was created in accordance with
the requirements of EN 1993-1-5 and modelled the geometry of an actual
physical test specimen that was tested in the 1980s. Chris Hendy said:
"Not only did the nonlinear LUSAS model give results almost
identical to the actual physical test specimen but it also showed that
the EN 1993-1-5 rules for stiffeners were very conservative for this
particular beam, and the BS 5400 Part 3 predictions even more
so."
Nonlinear modelling
of a plate girder in shear
Critical buckling
modelling
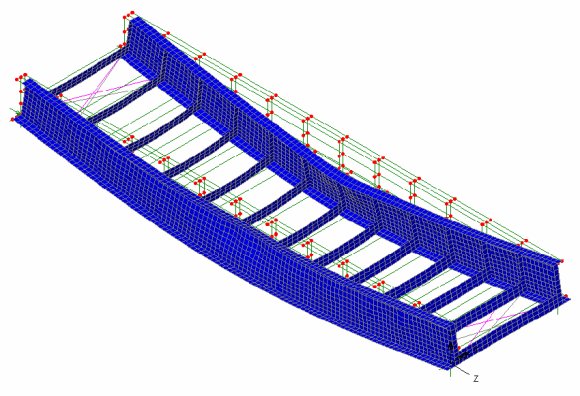
In another investigation, Atkins used
LUSAS Bridge to model a pair of steel beams during concrete placement,
prior to the concrete slab providing lateral restraint to the beams.
For this situation the new Eurocodes give no formula to derive the
critical bending moment. In LUSAS, thick shell elements represented
the plate girders, and beam elements modelled the bracing members. One span
was loaded with wet concrete such that the lateral torsional buckling
would govern the resistance of the beam group. From an eigenvalue
buckling analysis the critical buckling moment was seen to be caused
by the 20th mode, but at a load factor 50% greater than that predicted
by BS 5400.

Elastic critical
buckling analysis for a pair of braced beams (20th mode shape)
Nonlinear analysis
A nonlinear analysis carried out for
the same paired beams with material behaviour based upon Eurocode
recommendations, and with initial imperfections based on the elastic
critical buckling results, gave even better results. A collapse
deflection similar to that for elastic buckling was obtained but a
large increase in resistance was achieved by using nonlinear analysis
instead of the former linear analysis as shown in the results table.
This greater resistance could be attributed to a number of factors
including:
partial plastification of the tension zone; conservative code buckling
curves for this mode of buckling; and also redistribution of moment away
from the span to the supports.
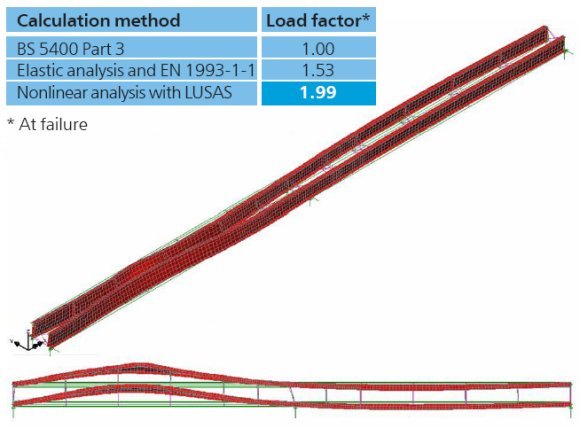
Nonlinear analysis of
a pair of braced beams
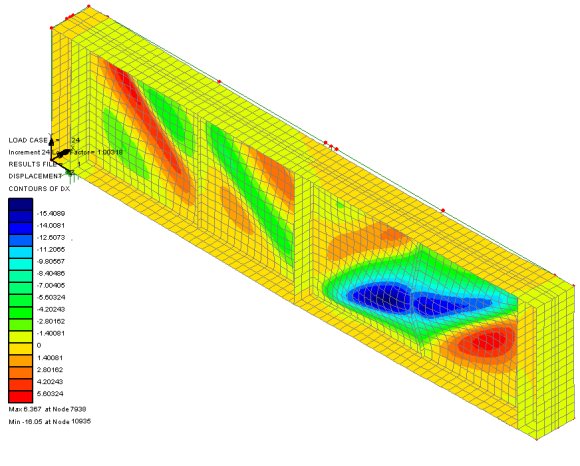
U-frame investigation
Atkins also examined the lateral
torsional buckling of U-frame bridge. Hand calculations using EN
1993-2 clause 6.3.4.2 and EN 1993-1-1 buckling curves gave a MbRk of
54358 kNm but by using LUSAS to run a nonlinear analysis the MbRk
value was increased to 72340 kNm. This was a significant improvement
over BS 5400 for several reasons: the effect of moment variation along
a beam is better accounted for; the partial plastification of the
tension zone is accounted for; and strain hardening allowed flange
stresses to increase about 7% above yield values.
Nonlinear analysis of
U-frame showing Ultimate Limit State collapse deflection
In summary
Elastic critical buckling analysis
using the new Eurocodes is more efficient than BS5400 Part
3. When linear buckling analysis is used comparable, and often more
beneficial results are obtained from using the Eurocodes, but when second-order effects are
considered using software with a nonlinear analysis capability, such
as that provided by LUSAS, even greater economy is achieved.
"Not only did the
nonlinear LUSAS model give results almost identical to the
actual physical test specimen but it also showed that the EN
1993-1-5 rules for stiffeners were very conservative for this
particular beam, and the BS 5400 Part 3 predictions even more
so."
Chris Hendy, Head
of Bridge Design and Technology, Atkins
Reference: Eurocode / BS 5400
comparison
|
|
EUROCODE part
|
Equivalent
BS 5400 part
|
|
|
- EN 1990 Basis of Structural
Design
|
BS
5400 Part 1 and 2
|
| ACTIONS
|
- EN 1991-1-1 Densities, self
weight and imposed loads
- EN 1991-1-4 Wind loads
- EN 1991-1-5 Thermal loads
- EN 1991-1-6 Actions during
excavation
- EN 1991-1-7 Accidental actions
- EN 1991-2 Traffic loads on
bridges
|
BS
5400 Part 2
|
| CONCRETE
|
- EN 1992-1-1 General rules and
rules for buildings
- EN 1992-2 Bridges
|
BS
5400 Part 4
|
| STEEL
|
- EN 1993-1-1General rules and
rules for buildings
- EN 1993-1-5 Plated structural
elements
- EN 1993-1-8 Design of joints
- EN 1993-1-9 Fatigue
- EN 1993-1-10 Brittle fracture
- EN 1993-2 Bridges
|
BS
5400 Part 3
|
| STEEL
- CONCRETE COMPOSITE
|
- EN 1994-2 General rules for
bridges
|
BS
5400 Part 5
|
Listing of Eurocode
parts needed in the design of a steel-concrete composite bridge
Find out more
Other LUSAS Bridge case studies:
|