Additional Information
See the Software Information
links for general details regarding LUSAS Bridge software products and
options.
Linear / Nonlinear Buckling Analysis

Buckling analysis of structures to
codified requirements is often over-conservative. For existing
structures, assessment or load rating to regional design codes
often shows they ‘fail’ buckling checks, but detailed buckling
analysis with LUSAS can often reveal additional ‘hidden’
capacity. For new plate girder, box or tub
girder bridge designs, linear and nonlinear buckling analysis
using LUSAS can investigate the girder stability during erection,
look at the effects of a slab casting sequence, and also help to
optimise the size of the web and flange plates, bracing,
stiffeners and position of any temporary supports used.
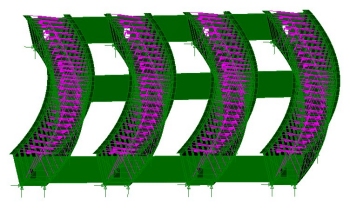
Linear buckling
To obtain an indication of a structure’s
potential to buckle under a particular loading a linear buckling
analysis can be undertaken. Linear buckling analysis can estimate
the maximum load that can be supported prior to structural instability
or collapse. A LUSAS analysis therefore provides load factors based on
classic elastic buckling. Where the type of structure isn’t covered by
the design code, and where P-delta, lift-off and yielding effects are
not significant in the loading range up to buckling, a linear buckling
analysis should give a more accurate assessment of member resistance
than would be obtained from a code of practice. However, imperfections
and nonlinearities tend to prevent most ‘real’ structures from
achieving their theoretical elastic (or "Euler") buckling
strength, so the eigenvalue buckling load factors are therefore somewhat
overestimated. To get a more accurate answer nonlinear analysis can be
undertaken.
|
|
|
|
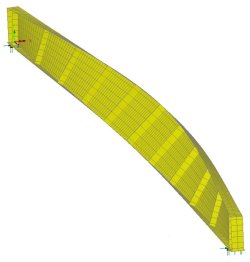
Nonlinear buckling
For a detailed structural buckling
assessment a geometrically nonlinear analyses should be carried out.
With this, material and boundary nonlinearity can also be investigated
if found to be required. With a geometrically nonlinear analysis the
stiffness matrix of the structure is automatically updated between
loading increments to incorporate deformations which affect the
structural behaviour (sometimes described by engineers as P-delta
effects).
Nonlinear buckling can be performed on the original structure
without imperfection, or by automatically adding an imperfection based
upon a scaled deformed shape which could be from a linear buckling
model.
|
|
|
A structure may also experience some
material nonlinearity during a buckling event (yielding for example)
and/or some boundary nonlinearity (lift-off supports, perhaps).
Generally it is recommended that modelling of nonlinear effects is done
progressively in order to evaluate the results of each additional
modelling at each stage. This helps in developing an understanding of
the structural behaviour and helps to identify the cause of any
potential failed analyses.
|
|
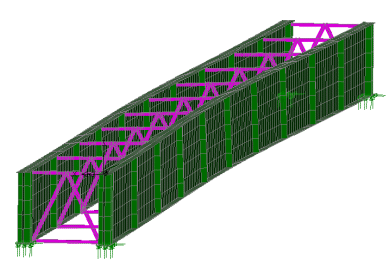
Erection
analysis
A nonlinear buckling analysis with
LUSAS can investigate the stability of girders under self-weight
loading, imposed construction loads such as slab pours, and wind
loads. From the results obtained, members can be re-sized
accordingly and, if necessary, temporary bracing and supports can
be inserted into the model and tested to reduce the structural
response.
For some clients, buckling analysis erection checks with
LUSAS have highlighted that for some open box girder designs with
narrow bottom flanges a standard design approach is just not
valid.
|

|
|
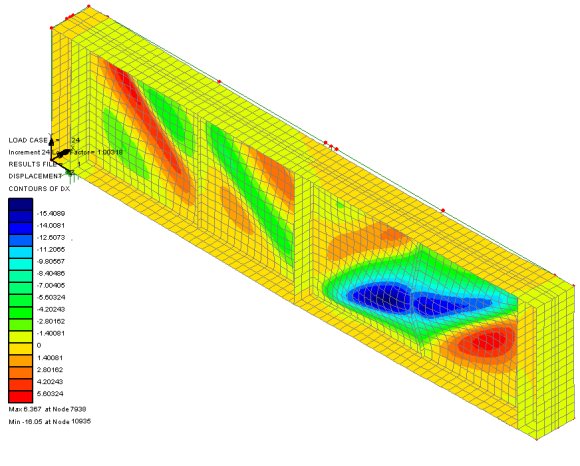
Mesh
sensitivity analysis
With finite element analysis, it is
good practice to carry out a mesh sensitivity check to ensure that
results are not unconservative. Mesh density should be checked to
ensure enough elements of the type chosen are being used. Coarse
mesh patterns could produce under conservative results; fine mesh
patterns may take longer to solve and be no more accurate.
Similarly quadratic elements will generally produce better results
than linear elements with nonlinear capabilities. Unlike some
software systems, with LUSAS, mesh patterns can be easily refined
and manipulated without losing any assigned supports and loading -
making it ideal for this type of work.
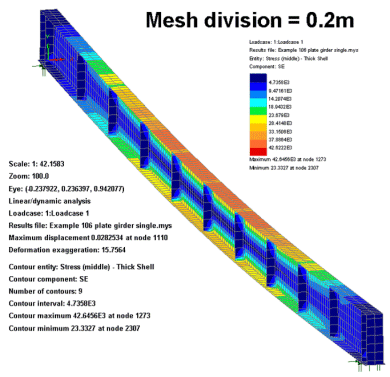
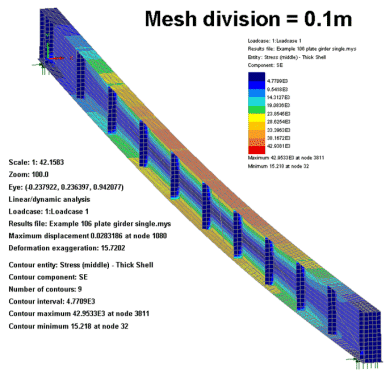
As an example the plate girder
shown was meshed with 0.2m mesh divisions and then had 0.1m mesh
divisions assigned for a mesh refinement check. The results showed
that the change of displacement and the difference in maximum
stress differed by less than 1% - meaning that, for this model at
least, the initial mesh definition was sufficiently fine enough to
achieve good results.
|
|
|
|
Nonlinear
buckling analysis procedure with LUSAS
- Carry-out an initial linear
analysis and check the stress levels for factored loading.
- Perform a mesh sensitivity
analysis
- Run a linear
eigenvalue buckling analysis to give load factor at which the
critical buckling may occur.
- Save the model and define an
initial imperfection (if necessary)
- Add nonlinear controls
- Run an initial geometric
nonlinear buckling analysis
- Add additional nonlinear
material or boundary conditions as necessary.
|
|
Buckling analysis
summary
- Linear buckling analysis enables
an assessment of the buckling resistance of a structure, and may
be particularly useful for structures not falling within the
scope of codes of practice.
- In some instances, a linear buckling
analysis may appropriate to satisfy checks against buckling, in
others, it may only provide a good starting point for a thorough
nonlinear buckling analysis.
- Nonlinear buckling analysis
provides a detailed buckling assessment and can include
geometric, material and boundary effects.
- LUSAS provides all the facilities
required for linear or nonlinear buckling analysis, and has the
ability to consider nonlinear buckling effects throughout a
staged erection analysis.
|
|
|
Software Information
|